200110 - 体育老师的乒乓球

上体育课时有m个同样的乒乓球，下课时用n个同样的筐子收集它们。假定任意一个筐子的容量都不小于m，若将收集的结果非降序排列，则排序后的序列有多少种可能？

一行，有单个空格分隔的的两个正整数，分别表示m和n。

对于40%的数据：

1\le m,n\le 1\le 100 。

对于80%的数据：

1\le m,n\le 1\le 200 。

对于100%的数据：

1\le m,n\le 1\le 300 。

一行，一个正整数。

按表中规律完成表格并思考：

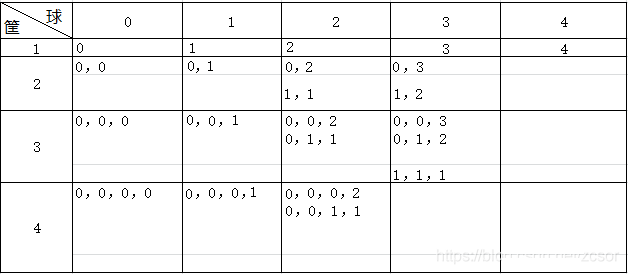
1、m < n 时的情况数和m个球m个筐子是否相同？

2、m >= n时的情况下：如果每个筐子都有球，那么各拿走1个球后，情况数发生变化吗？相反情况（不是每个筐子都有球）下，至少有1个筐子是空的，去掉它之后的情况数会发生变化吗？

用这样的思路递推出“数学方法”表达的递归函数：

#include<iostream>
using namespace std;

//函数功能：将m个球放在n个筐子里的放法 
//函数参数：m,n 
//返回值：放法总数 
//递归边界：m==0 || n==1
//递归过程：
//当m<n时，相当于m个球放在m个筐子。 
//当m>=n时，分两种情况：每个筐子都有球、有的筐子没有球 
long long ball(int m,int n){
	cout<<m<<" "<<n<<endl;
	//边界：0个球只有1种放法，1个筐子也只有1种放法 
	if(m==0) {
		return ____;
	}else if(n==1){
		return ____;
	}else if(m<n){			//筐子多的时候，和去掉空的一样。
		return ____;
	}else if(m>=n){			//分两部分：空着至少一个筐子；都有球
		//着重理解这部分代码是如何分治球比筐子多情况的：
		//1、都有球的情况可能更好理解：至少有1个球——拿掉这个球不影响放法数
		//2、相反情况（有空筐子）就好理解了：至少有1个空筐子——拿掉这个空筐子不影响放法数
		//但无论如何，都是让代码向着让问题规模变小的方向运行，最终达到递归边界。 
		return ____+____;
	}
}

int main(){
	int m,n;
	cin>>m>>n;
	cout<<ball(m,n)<<endl;
	return 0;
}

当填写完这些空格，你有一份可以得到正确答案的代码，但它还不够快，原因就是在递归过程中，有很多情况被多次重复计算：例如，当输入6 6 时，得到如下结果：

6 6
6 6
6 5
6 4
6 3
6 2
6 1
4 2
4 1
2 2
2 1
0 2
3 3
3 2
3 1
1 2
1 1
0 3
2 4
2 2
2 1
0 2
1 5
1 1
0 6

可以发现2 1 ，2 2 ，1 1,0 2等情况被重复计算若干次，当数据更大时，这些重复计算将更多，它们严重拖慢了程序速度。现在，尝试用一个二维数组记录已经计算过的情况的ans，当再次遇到这种情况时，直接从数组中取出ans来避免重复的计算。

虽然代码并不复杂，但当你完成这部分优化时，你的程序运行速度将提高非常多。

如果你有更多的精力和时间，可以思考这样一个问题：既然m,n较大时可以从较小的结果里面查询，那么是不是可以直接填表——从m=0,n=1开始，一直填写到m,n为输入的值时，arr[m][n]中保存的就是结果。