众所周知,魔术师通过一系列技巧来隐藏真相,魔术才成为魔术。有一种纸牌魔术,魔术师设计若干张纸牌,这些纸牌上的数字涵盖了从1到n的每个数字,每张纸牌正面有一组正整数a_{i_k},背面有一个序号i。魔术师通常会声称自己有超级记忆力:首先让一名观众记录这些纸牌上的一个数字,而后询问观众每张纸牌上是否有这个数字。当所有纸牌都被回答过一次“有”或“没有”之后,魔术师会说出观众所记录的数字是几。
该魔术的原理是对数字进行分类,其实施方式是使用二进制,于是可以通过计算快速得到答案。以一个较小的数字范围1~15为例:
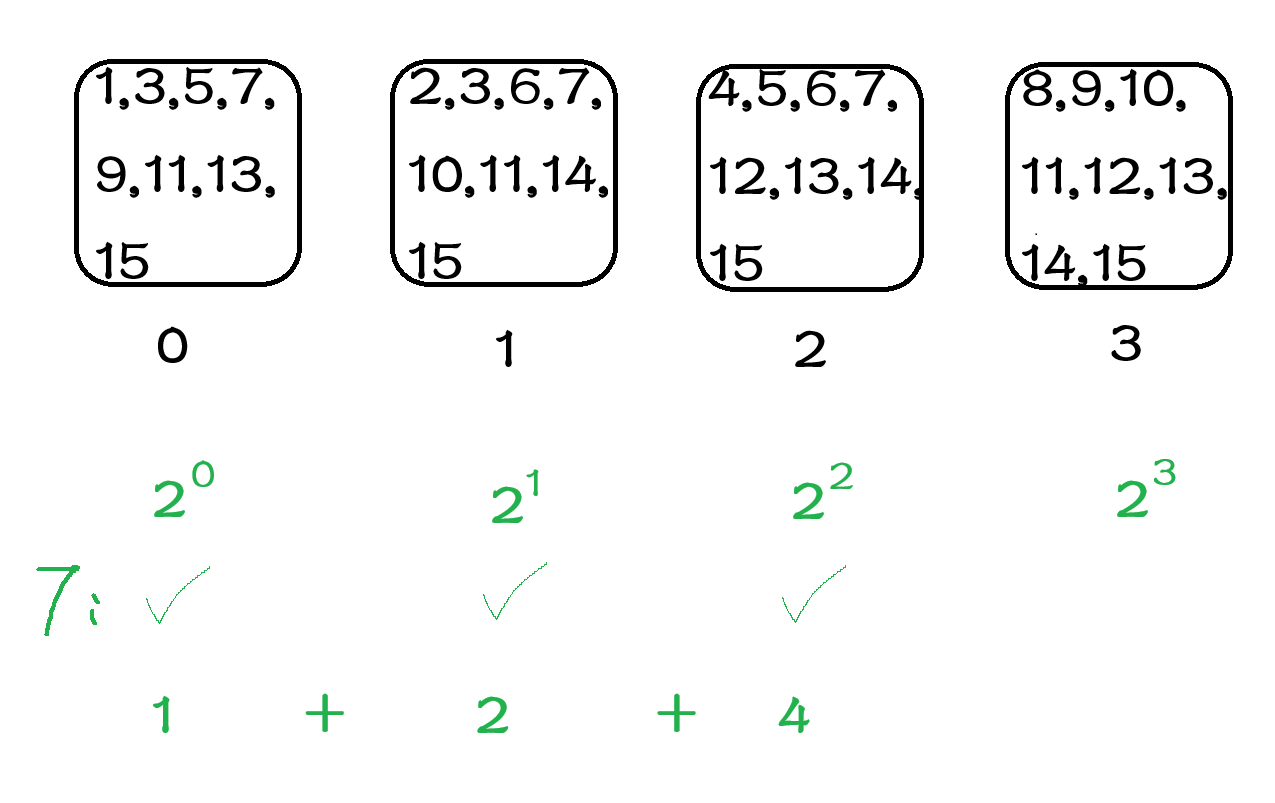
1、将每个数的二进制表示计算出来;
2、对于编号0的纸牌,其上的数字为2^0位上为1的全部数字,即[1, 3, 5, 7, 9, 11, 13, 15];
3、对于编号1的纸牌,其上的数字为2^1位上为1的全部数字,即[2, 3, 6, 7, 10, 11, 14, 15];
4、对于编号2的纸牌,其上的数字为2^2位上为1的全部数字,即[4, 5, 6, 7, 12, 13, 14, 15];
5、对于编号3的纸牌,其上的数字为2^3位上为1的全部数字,即[8, 9, 10, 11, 12, 13, 14, 15];
通常,多数魔术师会通过以下方法完成魔术:当观众回答所记录的数字在第i张纸牌上时,魔术师只需要记录二进制编号i的位置为1;若不在则该位置为0。而后将得到的二进制数转换为10进制即可。例如,观众记录了7这个数字,则魔术师得到0111这样一个二进制值,其对应的十进制值就是7。
当你得知真相之后,魔术似乎也不那么神奇了。给你一个数字n,你要从小到大按照编号从0到n-1输出每张纸牌的编号和上面的全部数字(同样按从小大顺序)。
一个正整数n。
对于100%的数据:
1\le n \le 10^5。
按i从小到大顺序输出若干行,每行开头为i:、接下来是若干个升序排列的由单个空格分隔的整数。
输入
15
输出
0:1 3 5 7 9 11 13 15 1:2 3 6 7 10 11 14 15 2:4 5 6 7 12 13 14 15 3:8 9 10 11 12 13 14 15
输入
16
输出
0: 1 3 5 7 9 11 13 15 1: 2 3 6 7 10 11 14 15 2: 4 5 6 7 12 13 14 15 3: 8 9 10 11 12 13 14 15 4: 16
该问题还有一个进阶版本,其内容完全相同,但时间限制为100毫秒,内存限制为16Mb。如果你的代码超出了这些限制,那么应该尝试优化你的代码。
