100707 - 素数筛

我们学习过素数判定方法——遍历可能的因数。但如果数据量很大就无法在规定时间内找出结果。素数筛可以解决这个问题，素数筛用于快速确定一定范围内哪些数是素数。它的基本思想是：

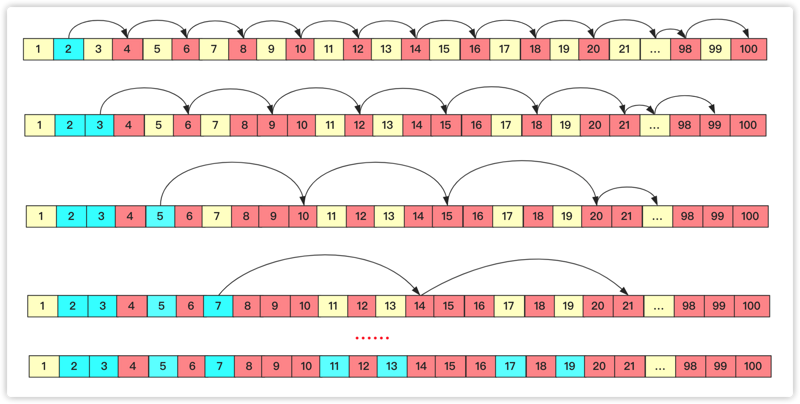
大于1的数不是素数就是合数，而合数可以被除了1和本身以外的数整除，于是2乘2、3、4……都是合数，3乘3、4、5……都是合数，5乘5、6、7……都是合数，没有被标记为合数的都是素数。这种巧妙的算法之所以效率好很多，是因为避免了每个数都需要单独验证而且把运算速度较慢的除法用乘法代替。当然，你有兴趣还可以考虑如何避免像18这样的数被计算了多次进一步提高效率。

现在，我们做一个关于素数筛的基础练习，这个练习只需要基本的素数筛算法就可以AC：

求从a到b有多少素数。

基本素数筛演示：

一行，用单个空格分隔的两个整数，分别表示a和b。

对于40%的数据：

1 \le a \le b \le 1\cdot 10^3

对于80%的数据：

1 \le a \le b \le 1\cdot 10^5

对于100%的数据：

1 \le a \le b \le 1\cdot 10^7

一行，一个整数，表示所求个数。