100000009 - Special Pythagorean triplet

毕达哥拉斯三元数指满足：a \lt b \lt c 且a^2+b^2=c^2的自然数集合。仅存在一组毕达哥拉斯三元数，使得a+b+c=n，求a×b×c。

n

测试点一：n=1000

测试点二：n=1998

一行由单个空格分隔的三个整数a×b×c。

这类问题的思路是充分利用题目信息，尽可能减少变量个数，尽可能增加变量限制，从而减少枚举次数。

a、设三角形周长为p，则有： a \lt p/3

将c=p-a-b带入a^2+b^2=c^2有：

b=(p^2-2pa)/(2p-2a)

从而，仅需一重循环枚举a∈[1,p/3]，再利用b为整数的性质就可以过滤掉很大部分，确定b之后，c随之确定问题解决。

b、利用欧几里得公式，以原题数据（1000）为例：

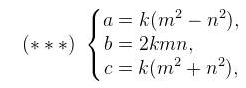
可以构造出勾股数，将其变形得：

a+b+c

=k(m^2-n^2+2mn+m^2+n^2)

=k(2m^2+2mn)

=2km(m+n)

=1000

显然，m∈[sqrt(250/k),sqrt(500/k)]，设k=1，则m的值仅可能为16、17、18、19、20、21，其中仅20是500的因子，于是m=20,n=5，得：

a=20^2-5^2=375

b=2×20×5=200

c=20^2+5^2=425

但需要注意的是，这种方法构造的a,b,c不一定是唯一的，很多时候还有其他数值与它们的和相等。例如1960对应着3组解：

560 588 812 267375360

392 735 833 240003960

245 840 875 180075000