100000002 - even Fibonacci numbers

斐波那契数列从第三项开始都是前两项和，若第一项与第二项为1、2，考虑该斐波那契数列中不超过n的项，求这些项中值为偶数项的和。

一行，一个整数。

测试点一：n=4×10^6

测试点二：n=10^{16}

a、其中2、5、8、11、14项为偶数（两基数相加得来），将f(n)=f(n-1)+f(n-2)变形：

=f(n-2)+f(n-3)+f(n-3)+f(n-4)

=2f(n-3)+f(n-2)+f(n-4)

=2f(n-3)+f(n-3)+f(n-4)+f(n-5)+f(n-6)

=3f(n-3)+f(n-4)+f(n-5)+f(n-6)

=3f(n-3)+f(n-3)-f(n-5)+f(n-5)+f(n-6)

=4f(n-3)+f(n-6)

得到偶数项递推公式：f(n)=4×f(n-3)+f(n-6)

换言之，有一个数列，其第一项为2，第二项为8，递推公式为f(n)=4×f(n-1)+f(n-2)。

b、使用斐波那契数列通项公式，依次求出并筛选符合题意的斐波那契数。但遗憾的是，斐波那契数列的通项公式比其递推公式难于用程序高效实现，它长这个样子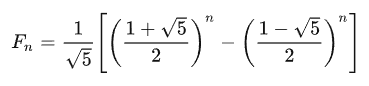： 小数的累加导致误差不断累积，用高精实现效率又较低。